1. Tranches de tableaux et points de suspension▲
Nous avons vu la dernière fois que l'on pouvait utiliser des tranches pour accéder à des lignes ou des colonnes entières de tableaux NumPy, mais j'ai laissé provisoirement de côté une facilité syntaxique, les points de suspension (...). Nous avons vu que nous pouvions enlever les dimensions qui ne sont pas nécessaires avec le caractère deux-points (:) ; et si nous avons besoin de la dernière dimension, nous pouvons omettre le deux-points :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
>>> a = np.arange(10, 40).reshape(3,5,2)
>>> a
array([[[10, 11],
[12, 13],
[14, 15],
[16, 17],
[18, 19]],
[[20, 21],
[22, 23],
[24, 25],
[26, 27],
[28, 29]],
[[30, 31],
[32, 33],
[34, 35],
[36, 37],
[38, 39]]])
>>> a[:, 1, :]
array([[12, 13],
[22, 23],
[32, 33]])
>>> a[:, 1]
array([[12, 13],
[22, 23],
[32, 33]])
En utilisant des points de suspension (...), nous pouvons représenter autant de dimensions que nécessaire pour produire le tuple d'indexation complet :
2.
3.
4.
5.
6.
7.
8.
>>> a[:, :, 1]
array([[11, 13, 15, 17, 19],
[21, 23, 25, 27, 29],
[31, 33, 35, 37, 39]])
>>> a[...,1]
array([[11, 13, 15, 17, 19],
[21, 23, 25, 27, 29],
[31, 33, 35, 37, 39]])
Pour les petites dimensions, cela ne fait guère de différence, mais si vous avez des dimensions plus grandes, vous avez moins de code à taper pour obtenir les données dont vous avez besoin.
2. Indexation avec des tableaux de booléens▲
L'indexation se fait habituellement avec des indices numériques. NumPy va plus loin et permet l'indexation au moyen de tableaux de booléens. L'idée derrière cela est qu'un tel tableau booléen fonctionne comme un filtre. Nous définissons un tableau de booléens pour indiquer à NumPy les nombres dont nous avons besoin (True) et ceux dont nous n'avons pas besoin (False) :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
>>> a = np.arange(10, 40).reshape(5,6)
>>> a
array([[10, 11, 12, 13, 14, 15],
[16, 17, 18, 19, 20, 21],
[22, 23, 24, 25, 26, 27],
[28, 29, 30, 31, 32, 33],
[34, 35, 36, 37, 38, 39]])
>>> idx = np.array([[True, False, True, False, True, False],
[True, False, True, False, True, False],
[True, False, True, False, True, False],
[True, False, True, False, True, False],
[True, False, True, False, True, False]
], dtype=bool)
>>> a[idx]
array([10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38])
Dans l'exemple ci-dessus, nous avons créé un tableau NumPy contenant des valeurs booléennes. Maintenant, si nous fournissons ce tableau booléen comme un paramètre d'indexation à un autre tableau NumPy (qui a les mêmes dimensions), nous filtrons le contenu du tableau et obtenons un vecteur (matrice unidimensionnelle) contenant les valeurs pour lesquelles l'indice est à True.
Nous pouvons également fournir un tableau ayant une forme un peu différente pour l'indexation, mais cela génère un avertissement :
2.
3.
4.
5.
6.
7.
>>> idx = np.array([[True, False, True, False, True, False],
[True, False, True, False, True, False],
[True, False, True, False, True, False]
], dtype=bool)
>>> a[idx]
__main__:1: VisibleDeprecationWarning: boolean index did not match indexed array along dimension 0; dimension is 5 but corresponding boolean dimension is 3
array([10, 12, 14, 16, 18, 20, 22, 24, 26])
L'avertissement nous indique que nous avons fourni un tableau de forme incorrecte pour l'index – mais nous récupérons toutes les valeurs que nous voulons obtenir : NumPy interprète les dimensions manquantes comme complètement remplies avec False.
Maintenant que nous savons utiliser des tableaux de booléens pour l'indexation, nous pouvons aller plus loin et filtrer les valeurs, non plus en générant manuellement des tableaux de booléens mais en laissant à NumPy le soin d'en assurer la création :
2.
3.
4.
5.
6.
7.
8.
9.
>>> idx = a > 25
>>> idx
array([[False, False, False, False, False, False],
[False, False, False, False, False, False],
[False, False, False, False, True, True],
[ True, True, True, True, True, True],
[ True, True, True, True, True, True]], dtype=bool)
>>> a[idx]
array([26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39])
Dans cet exemple, nous demandons à NumPy de construire un tableau de booléens afin de ne garder que les valeurs qui sont supérieures à 25.
3. Chargement de contenu hétérogène▲
Nous avons vu dans la section précédente que nous pouvons créer des tableaux de types non numériques (comme des booléens). Il est maintenant temps d'utiliser ces connaissances et de charger un fichier CSV (Comma Separated Values, valeurs séparées par des virgules) avec un contenu hétérogène.
Pour cela, nous allons utiliser un jeu de données sur les prénoms de bébé les plus populaires, regroupés par sexe et appartenance ethnique de la mère, dans la ville de New York (Most Popular Baby Names by Sex and Mother's Ethnic Group, New York City). J'ai téléchargé la version CSV et l'ai appelée baby_names.csv. Ainsi vous pouvez suivre et tester vous-même les exemples sur le jeu de données.
Le fichier a l'en-tête suivant :
BRTH_YR,GNDR,ETHCTY,NM,CNT,RNKce qui correspond aux libellés de champs suivants :
- Année de naissance
- Genre
- Origine ethnique
- Prénom
- Fréquence
- Rang
Commençons par charger le fichier avec NumPy comme nous l'avons appris dans l'article précédent :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
>>> baby_names = np.genfromtxt('baby_names.csv', skip_header=True, delimiter=",")
>>> baby_names
array([[ 2011., nan, nan, nan, 13., 75.],
[ 2011., nan, nan, nan, 21., 67.],
[ 2011., nan, nan, nan, 49., 42.],
...,
[ 2014., nan, nan, nan, 16., 96.],
[ 2014., nan, nan, nan, 90., 39.],
[ 2014., nan, nan, nan, 49., 65.]])
>>> baby_names.shape
(13962, 6)
L'exemple vous montre ce qui se passe si nous utilisons le type de données par défaut (float) pour les tableaux NumPy : on obtient beaucoup de champs renseignés à nan, ce qui signifie not a number (pas un nombre). Effectivement, l'échantillon de données se compose de beaucoup de chaînes de caractères qui ne peuvent pas être converties en float.
Essayons de charger l'information dans un format adéquat :
2.
3.
4.
5.
6.
7.
8.
9.
10.
>>> baby_names = np.genfromtxt('baby_names.csv', skip_header=True, delimiter=",", dtype='U75')
>>> baby_names
array([['2011', 'FEMALE', 'HISPANIC', 'GERALDINE', '13', '75'],
['2011', 'FEMALE', 'HISPANIC', 'GIA', '21', '67'],
['2011', 'FEMALE', 'HISPANIC', 'GIANNA', '49', '42'],
...,
['2014', 'MALE', 'WHITE NON HISPANIC', 'Yusuf', '16', '96'],
['2014', 'MALE', 'WHITE NON HISPANIC', 'Zachary', '90', '39'],
['2014', 'MALE', 'WHITE NON HISPANIC', 'Zev', '49', '65']],
dtype='<U75')
La différence est que j'ai ajouté l'argument dtype à la fonction genfromtxt. La valeur U75 spécifie que nous voulons lire des chaînes Unicode de 75 caractères.
L'argument skip_header spécifie que nous voulons ignorer l'en-tête, qui est la première ligne du fichier CSV.
L'inconvénient de cette approche est que l'on obtient chaque colonne sous la forme d'une chaîne de caractères, même pour les valeurs numériques. En effet, NumPy exige que chaque élément soit du même type, il n'a donc pas besoin de vérifier les types à chaque fois, ce qui accélère le traitement de gros volumes de données.
Naturellement, il y a une solution si vous voulez convertir une colonne en nombre parce que vous voulez effectuer des calculs dessus. Par exemple, calculons les noms des bébés masculins et féminins en 2011 :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
>>> year_filter = baby_names[:,0] == '2011'
>>> female_filter = baby_names[:,1] == 'FEMALE'
>>> male_filter = baby_names[:,1] == 'MALE'
>>> male_2011 = year_filter & male_filter
>>> female_2011 = year_filter & female_filter
>>> baby_names[female_2011]
array([['2011', 'FEMALE', 'HISPANIC', 'GERALDINE', '13', '75'],
['2011', 'FEMALE', 'HISPANIC', 'GIA', '21', '67'],
['2011', 'FEMALE', 'HISPANIC', 'GIANNA', '49', '42'],
...,
['2011', 'FEMALE', 'WHITE NON HISPANIC', 'ZISSY', '25', '66'],
['2011', 'FEMALE', 'WHITE NON HISPANIC', 'ZOE', '81', '28'],
['2011', 'FEMALE', 'WHITE NON HISPANIC', 'ZOEY', '21', '70']],
dtype='<U75')
>>>
>>> female_count = np.sum(baby_names[(female_2011), -2].astype(int))
>>> male_count = np.sum(baby_names[(male_2011), -2].astype(int))
>>> female_count
117948
>>> male_count
153748
>>> np.sum(baby_names[(year_filter), -2].astype(int))
271696
>>> female_count+male_count
271696
Comme vous pouvez le voir, j'ai créé des filtres qui peuvent être utilisés plus tard avec le tableau de base pour ne sélectionner que les valeurs qui nous intéressent. Je divise les filtres en parties élémentaires (year_filter, female_filter, male_filter) puis combine ces filtres élémentaires pour former des filtres composites (female_2011, male_2011).
La sélection baby_names [(female_2011), -2] recherche toutes les lignes contenant des prénoms féminins du jeu de données et récupère seulement l'avant-dernière colonne, qui est la fréquence de ces prénoms. Une fois cette option sélectionnée, nous pouvons convertir les valeurs de ce vecteur (la colonne sélectionnée) en un entier avec l'appel de la méthode .astype (int). Enfin, nous sommons les résultats.
Enfin, j'ai également ajouté des lignes de code pour vérifier que nous avions sélectionné les bonnes valeurs et que nous n'avions dans notre jeu de données aucun cas où le genre serait manquant.
4. Vues et copies▲
Nous arrivons maintenant à un sujet qui peut être source de confusion pour l'utilisateur débutant de NumPy : quand un tableau est-il copié ? Voyons un exemple simple avec Python :
2.
3.
4.
5.
6.
7.
>>> a = [1,2,3,4,5,6]
>>> b = a
>>> a is b
True
>>> b[2] = 11
>>> a
[1, 2, 11, 4, 5, 6]
Et faisons maintenant de même avec NumPy :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
>>> import numpy as np
>>> a = np.array([1,2,3,4,5,6])
>>> b = a
>>> a is b
True
>>> a.shape
(6,)
>>> b.shape = 3,2
>>> a
array([[1, 2],
[3, 4],
[5, 6]])
Comme vous pouvez le constater, lorsque nous avons assigné la valeur de a à b, nous n'avons pas créé de copie du contenu de la variable a, mais donné à la nouvelle variable b une valeur qui est une référence au contenu d'origine de la variable a. Si nous changeons quelque chose dans la nouvelle variable b (par exemple la forme ou le contenu), ce changement se répercute sur la variable d'origine a.
Vous pouvez obtenir un comportement différent avec des vues sur le tableau d'origine :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
>>> import numpy as np
>>> a = np.array([1,2,3,4,5,6])
>>> b = a.view()
>>> b
array([1, 2, 3, 4, 5, 6])
>>> b.shape = 2,3
>>> b
array([[1, 2, 3],
[4, 5, 6]])
>>> a
array([1, 2, 3, 4, 5, 6])
Mais attention : l'utilisation de la méthode view() sur les tableaux crée une copie qui fait référence aux éléments du tableau d'origine ; changer la forme n'a aucun effet sur l'original mais il en va différemment si l'on modifie les valeurs :
2.
3.
4.
5.
6.
7.
8.
9.
>>> b[0, 2]
3
>>> b[0, 2] = 12
>>> a
array([ 1, 2, 12, 4, 5, 6])
>>> b.flags.owndata
False
>>> b.base is a
True
Si vous regardez le fragment de code ci-dessus, vous pouvez voir que modifier une valeur dans b modifie également la valeur dans a, même si les tableaux ont des formes différentes. On peut en voir la raison dans l'indicateur owndata du nouveau tableau b — il ne possède pas de données en propre, il partage les données de l'original a.
Si vous voulez vraiment une copie qui ne partage pas les données, vous pouvez utiliser la méthode copy() :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
>>> a
array([ 1, 2, 12, 4, 5, 6])
>>> b = a.copy()
>>> b.base is a
False
>>> b.flags.owndata
True
>>> b.shape = 2,3
>>> b[0,0] = 11
>>> a
array([ 1, 2, 12, 4, 5, 6])
>>> b
array([[11, 2, 12],
[ 4, 5, 6]])
Maintenant nous avons un nouveau tableau b vraiment indépendant dont le contenu reflète l'état du tableau a lors de l'appel de copy(), et les deux variables ne sont plus liées.
5. Arithmétique▲
Si vous effectuez une opération arithmétique sur un tableau NumPy, celle-ci s'appliquera à tous les éléments du tableau et un nouveau tableau est créé avec les résultats.
En fait, il n'y a pas grand-chose à ajouter à ce sujet ; nous utiliserons simplement les opérateurs arithmétiques de base :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
>>> import numpy as np
>>> a = np.array([1,2,3,4,5,6])
>>> a + 4
array([ 5, 6, 7, 8, 9, 10])
>>> array * 5
array([ 5, 10, 15, 20, 25, 30])
>>> a - 10
array([-9, -8, -7, -6, -5, -4])
>>> a / 2
array([ 0.5, 1. , 1.5, 2. , 2.5, 3. ])
>>> a // 2
array([0, 1, 1, 2, 2, 3])
Si nous utilisons les opérateurs d'affectation modifiée (comme += ou *=), nous obtenons les mêmes résultats : le tableau est modifié sur place et l'opération est effectuée sur tous les éléments du tableau :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
>>> a = np.array([1,2,3,4,5,6])
>>> a += 4
>>> a
array([ 5, 6, 7, 8, 9, 10])
>>> a *= 5
>>> a
array([25, 30, 35, 40, 45, 50])
>>> a -= 10
>>> a
array([15, 20, 25, 30, 35, 40])
>>> a //= 2
>>> a
array([ 7, 10, 12, 15, 17, 20])
>>> a = np.array([ 7, 10, 12, 15, 17, 20], dtype=float)
>>> a
array([ 7., 10., 12., 15., 17., 20.])
>>> a /= 2
>>> a
array([ 3.5, 5. , 6. , 7.5, 8.5, 10. ])
Comme vous pouvez le voir, pour utiliser l'opérateur d'affectation avec division /=, vous devez convertir le tableau en dtype capable de gérer les nombres à virgule flottante.
Cependant, il existe certaines fonctions dans NumPy qui convertissent directement les matrices d'éléments entiers en matrices à virgule flottante :
2.
3.
4.
5.
6.
7.
8.
>>> a = np.array([ 7, 10, 12, 15, 17, 20])
>>> a.dtype
dtype('int64')
>>> np.sin(a)
array([ 0.6569866 , -0.54402111, -0.53657292, 0.65028784, -0.96139749,
0.91294525])
>>> np.sin(a).dtype
dtype('float64')
6. Tracer les histogrammes▲
Certes, ce sujet ne fait pas vraiment partie de NumPy puisqu'il faut une bibliothèque supplémentaire.
Cependant, ce tutoriel ne concerne pas le traçage. Par conséquent, nous allons seulement créer un histogramme simple basé sur les informations de prénoms de bébé utilisés dans ce tutoriel. Nous allons représenter le nombre de prénoms en 2012 pour chaque origine ethnique.
2.
3.
4.
5.
6.
7.
8.
>>> year_2012 = baby_names[:, 0] == '2012'
>>> ethnicities = np.unique(baby_names[(year_2012), 2])
>>> for e in ethnicities:
... ethnicity_filter = baby_names[:,2] == e
... sums[e] = np.sum(baby_names[(year_2012 & ethnicity_filter), -2].astype(int))
...
>>> sums
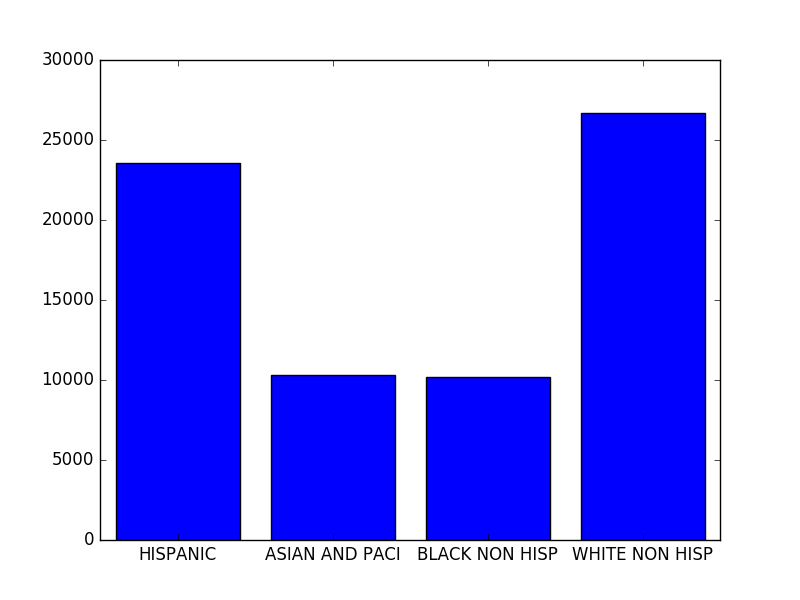
{'HISPANIC': 23547, 'ASIAN AND PACI': 10300, 'BLACK NON HISP': 10208, 'WHITE NON HISP': 26675}
Comme vous pouvez le voir, nous avons stocké les résultats dans le dictionnaire sums pour avoir une relation entre les ethnies et nombres de prénoms.
C'est une approche possible, mais on peut aussi le faire autrement. Par exemple, filtrez tout le jeu de données dès le début et n'utilisez que les lignes contenant des données de 2012 plus tard (comme lorsque nous avons calculé les ethnies uniques).
La dernière étape est le traçage lui-même. Nous créons un histogramme en utilisant matplotlib ; la hauteur de chaque rectangle est définie par le décompte du nombre de prénoms pour chaque ethnie donnée (les valeurs du dictionnaire sums).
Et le résultat est semblable à ceci :
7. Conclusion▲
Nous avons terminé cette introduction à NumPy avec quelques sujets avancés. Nous avons vu que la performance de NumPy est meilleure si nous avons toutes les données du même type, ce qui signifie que nous avons parfois des colonnes numériques sous la forme de chaînes de caractères dans notre matrice.
8. Remerciements▲
Nous remercions Gabor Laszlo Hajba de nous avoir autorisés à publier son tutoriel NumPy Advanced Topics.
Nous tenons également à remercier Lolo78 pour la traduction de ce tutoriel, Laethy pour la revue de la traduction et f-leb pour la relecture orthographique.